کیان آنلاین؛ اگر زندگی خود را با پیشینیان خود مقایسه کنید، متوجه میشوید که اغلب در گذر زمان، استانداردها به صورت قابلتوجهی برای اغلب خانوادهها در بسیاری از کشورها، افزایش پیدا کردهاند. منشاء این پیشرفت، درآمد افزایش یافته است و این امکان را برای افراد بوجود میآورد که کالاها و خدمات بیشتری را مصرف کنند. برای سنجش رشد اقتصادی، اقتصاددانان از دادههای تولید ناخالص داخلی استفاده میکنند که میزان کل درآمد هر فرد در اقتصاد یک کشور را اندازهگیری میکند. برای مثال، رشد جی دی پی حقیقی در مقایسه با سال ۱۹۵۰ میلادی در ایالات متحده آمریکا، افزایش چشمگیری را تجربه کرده است. همچنین، در هر سال معین، تفاوت قابل توجهی در استاندارد زندگی میان کشورهای مختلف مشاهده میٰشود.
در جدول زیر میتوانید درآمد سرانه در سال ۲۰۱۲ میلادی را در ۴ کشور پرجمعیت جهان، مشاهده کنید. ایالات متحده آمریکا با درآمد سرانه ۵۱۷۴۹ دلار در صدر قرار دارد. درآمد سرانه در همین سال در اتیوپی معادل ۱۲۴۰ دلار بوده است. عوامل بوجود آورنده این تفاوتها در درآمد در طی زمان و در کشورهای متفاوت در مبحث رشد اقتصادی، مورد بررسی قرار میگیرد.
| درآمد سرانه در سال ۲۰۱۲ میلادی | کشور |
| ۵۱۷۴۹ | ایالات متحده آمریکا |
| ۳۵۶۱۸ | ژاپن |
| ۱۰۹۶۰ | چین |
| ۴۴۳۷ | پاکستان |
عوامل تعیین کننده رشد اقتصادی چه هستند؟
همانطور که میدانید عوامل تولید، نیروی کار و نیروی سرمایه هستند و به همراه «فناوری تولید» (Production Technology)، منبع تولید و درآمد یک کشور را تشکیل میدهند. بنابراین تغییرات درآمدی در زمانها و کشورهای مختلف در نتیجه تفاوتهای موجود در سرمایه، نیروی کار و فناوری بوجود میآیند. در ادامه، نظریه رشد اقتصادی تحت عنوان «مدل رشد سولو» (Solow Growth Model) بررسی میشود. با توسعه این مدل، تحلیل پویاتر میشود، مانند اینکه فیلمی را تحلیل کنیم و نه یک عکس را. مدل رشد سولو نشاندهنده چگونگی تاثیرگذاری رشد جمعیت پساندازکننده و پیشرفت فناوری، بر سطح تولید یک اقتصاد و رشد آن در طی زمان است.
انباشت سرمایه و مدل رشد سولو
مدل رشد سولو طراحی شده است که نشاندهنده چگونگی تاثیرپذیری و تعامل رشد سرمایه انباشتهشده، رشد در نیروی کار و توسعه فناوری در اقتصاد با یکدیگر باشد و این که این موارد چه تاثیری بر میزان کل تولید کالاها و خدمات یک کشور، دارند. در ادامه این مطلب، مدل سولو را بیشتر بررسی خواهیم کرد.در اولین گام تحقیق میکنیم که چگونه عرضه و تقاضا کالا، تعیینکننده میزان سرمایه انباشتهشده هستند. در ابتدا، فرض میکنیم که نیروی کار و فناوری، ثابت باشند.
عرضه و تقاضای کالاها
عرضه و تقاضا برای کالاها، نقش مهمی در مدل سولو ایفا میکنند. با توجه به عرضه و تقاضای کالاها، میتوانیم متوجه شویم که چه موردی تعیینکننده میزان تولیدات بدست آمده در هر زمان معین و تخصیص آن در میان کاربردهای جایگزین است.
عرضه کالاها و تابع تولید
عرضه کالاها در مدل سولو بر پایه تابع تولید است که نشاندهنده این است که میزان تولید بستگی به سرمایه و نیروی کار دارد.
Y=F(K,L)Y=F(K,L)
مدل رشد سولو فرض میکند که تابع تولید، بازدهی ثابت به مقیاس دارد. این فرض عموماً واقعگرایانه در نظر گرفته میشود و همچنین، به آسان بودن تحلیل، کمک میکند. توجه داشته باشید که هر تابع تولیدی در صورت مثبت بودن عدد zz، دارای بازدهی نسبت به مقیاس ثابت است.
zY=F(zK,zL)zY=F(zK,zL)
یعنی، اگر سرمایه و نیروی کار هر دو در zz ضرب شوند، میزان تولید نیز در zz ضرب خواهد شد. توابع تولید با بازده ثابت به مقیاس، امکان تحلیل تمام مقادیر در اقتصاد را در نسبت به اندازه نیروی کار، فراهم میکند. برای بررسی صحت آن در z=1Lz=1L، معادله به شکل زیر بدست میآید.
YL=F(KL,1)YL=F(KL,1)
معادله بالا نشاندهنده آن است که میزان تولید به ازای هر نیروی کار YLYL تابعی از میزان سرمایه به ازای نیروی کار (KLKL) است. توجه داشته باشید که عدد ۱ ثابت است و میتوان از آن چشمپوشی کرد. فرض بازدهی ثابت نسبت به مقیاس، نشاندهنده این است که اندازه اقتصاد – اندازهگیری شده توسط نیروی کار – بر رابطه میان میزان محصول به ازای نیروی کار و میزان سرمایه به ازای نیروی کار تاثیری ندارد.
به علت کم اهمیت بودن اندازه اقتصاد، تمام مقادیر را به صورت «به ازای نیروی کار» (Per Worker) اعلام میشوند. مقادیر به ازای نیروی کار را با حروف کوچک نشان میدهیم. برای مثال yy را برابر y=YLy=YL و k=KLk=KL معادل سرمایه به ازای نیروی کار در نظر میگیریم. بنابراین، میتوان تابع تولید را به صورت زیر نوشت.
y=f(k)y=f(k)
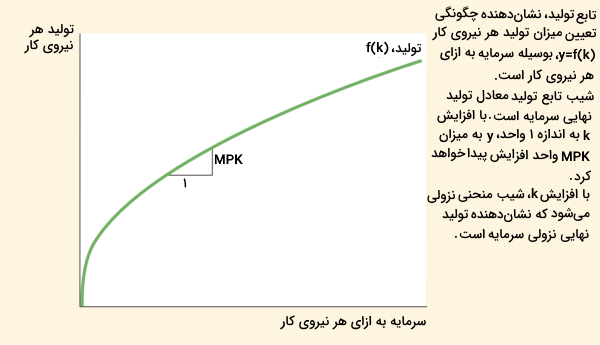
در معادله بالا، f(k)=F(k,1)f(k)=F(k,1) برقرار است. در تصویر زیر میتوانید نمودار این تابع را مشاهده کنید. شیب نمودار این تابع تولید نشاندهنده این است که با اضافه شدن یک واحد سرمایه، چه مقدار اضافهای توسط نیروی کار تولید میشود. این مقدار، تولید نهایی سرمایه (MPKMPK) نام دارد که به صورت ریاضی به شکل زیر نوشته میشود.
MPK=f(k+1)−f(k)MPK=f(k+1)−f(k)
توجه داشته باشید که در نمودار زیر با افزایش میزان سرمایه، از شیب تابع تولید کاسته میشود. یعنی تابع تولید نشاندهنده کاهنده بودن تولید نهایی سرمایه است. زمانی که kk مقدار اندکی است، نیروی کار متوسط میزان کمی سرمایه برای تولید در اختیار دارد. در نتیجه، افزودهشدن مقدار بیشتری سرمایه بسیار کاربردی خواهد بود و تولید را به میزان قابلتوجهی افزایش خواهد داد. در زمان بالا بودن kk، نیروی کار متوسط به مقدار زیادی سرمایه دسترسی دارد. در نتیجه، افزایش یک واحدی سرمایه تنها به میزان کمی تولید را زیاد میکند.
تقاضا برای کالاها و تابع مصرف
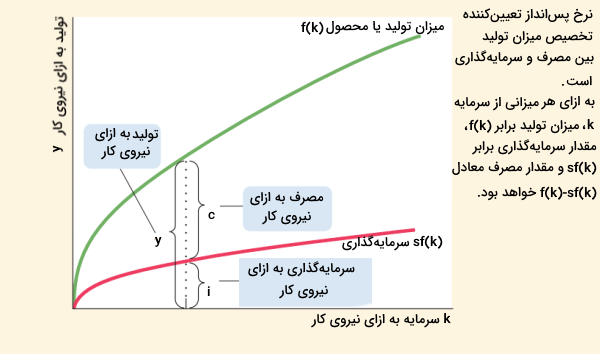
منشا تقاضا در مدل سولو، مصرف و سرمایهگذاری هستند. به عبارتی دیگر، میزان تولید به ازای نیروی کار yy، از مصرف به ازای نیروی کارcc و سرمایهگذاری به ازای نیروی کارii بدست میآید.
y=c+iy=c+i
این معادله نسخه به ازای نیروی کار حسابهای درآمد ملی برای یک اقتصاد است. توجه داشته باشید که در این معادله، مخارج دولت (برای سادگی بیشتر) و خالص صادرات (به علت بستهبودن اقتصاد) در نظر گرفته نشدهاند. مدل سولو فرض میکند که هرسال، افراد، کسری از درآمد خود را پسانداز (ss) و کسری دیگر را مصرف میکنند.
میتوانیم با تابع مصرف، این ایده را به شکل زیر نمایش دهیم.
c=(1−s)yc=(1−s)y
در معادله بالا، ss یا نرخ پسانداز، عددی بین صفر و ۱ است. توجه داشته باشید که احتمال دارد سیاستهای مختلف دولتی بر نرخ پسانداز در جامعه تاثیرگذار باشد. بنابراین، یکی از هدفها این است که نرخ پسانداز مطلوب را بیابیم. البته فعلاً در این بخش، نرخ پسانداز را برونزا در نظر میگیریم. برای دیدن اینکه تابع مصرف معرفیشده، نشاندهنده سرمایهگذاری نیز هست، در معادله حساب درآمد ملی، به جای مصرف یا cc، باید (s−1)y−(s−1)y− را قرار دهیم.
y=(1−s)y+iy=(1−s)y+i
عبارت را به صورتی تغییر میدهیم که به معادله زیر دست پیدا کنیم.
i=syi=sy
معادله بالا، نشاندهنده برابری سرمایهگذاری با پسانداز است. همچنین، نرخ پسانداز یا ss نیز، کسری از میزان محصول اختصاص داده شده به سرمایهگذاری است. تا اینجا، ۲ عامل اصلی تشکیلدهنده مدل سولو – تابع تولید و تابع مصرف – را معرفی کردهایم. برای هر میزان سرمایه داده شده (kk)، تابع تولید y=f(k)y=f(k) نشاندهنده میزان محصولات تولیدشده در هر اقتصاد و نرخ پسانداز ss نشاندهنده میزان تخصیص آن محصول به مصرف و سرمایهگذاری است.
رشد میزان سرمایه و حالت پایدار ثابت
در هر لحظه، میزان انباشت سرمایه، عاملی تعیینکننده در تولید اقتصاد به شمار میرود. امکان تغییر میزان سرمایه انباشته شده در طی زمان وجود دارد و این تغییرات میتوانند رشد اقتصادی را به همراه داشته باشند. به صورت جزئی، میتوان گفت که ۲ عامل سرمایهگذاری و «استهلاک» (Depreciation) بر میزان انباشت سرمایه، تاثیرگذار هستند. سرمایهگذاری همان خریداری دستگاهها، ماشینآلات و تجهیزات تولیدی جدید است و بیشتر شدن سرمایه انباشتهشده را به همراه دارد.
استهلاک، درواقع، از بین رفتن سرمایهها و قدیمی شدن و از کارافتادن آنها به علت گذر زمان و استفاده بیش از حد است. در اینجا، تاثیر این موارد را به ترتیب بررسی میکنیم. همانطور که بالاتر بیان شد، میزان سرمایه به ازای نیروی کار (ii) برابر sysy است. با قراردادن تابع تولید به جای yy، میتوانیم میزان «سرمایهگذاری» (Investment) به ازای نیروی کار را به عنوان تابعی از میزان «سرمایه» (Capital) به ازای نیروی کار، تعریف کنیم.
i=sf(k)i=sf(k)
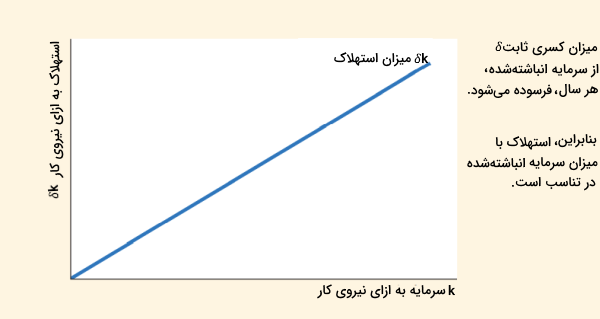
معادله بالا، نشاندهنده ارتباط میان میزان سرمایه فعلی (kk) با جمعآوری میزان سرمایه جدید (ii) است. در نمودار زیر میتوانید این رابطه را مشاهده کنید. در این نمودار قابل ملاحظه است که چگونه برای هر مقداری از kk میزان محصول به ازای تابع تولید (f(k)f(k)) مشخص میشود. همچنین، تخصیص میزان تولید میان مصرف و سرمایهگذاری توسط نرخ پسانداز (ss) معین میگردد. برای در نظر گرفتن استهلاک در مدل، فرض میکنیم که درصد معینی از سرمایه (δδ) هرساله مستهلک شود. بنابراین، δδ نشاندهنده نرخ استهلاک است. برای مثال، اگر سرمایه برای ۲۵ سال قابلیت کارایی داشته باشد، نرخ استهلاک سالیانه برابر ۰٫۰۴ خواهد بود.
مقدار سرمایهای که هرسال مستهلک میشود برابر δkδk خواهد بود. در نمودار زیر قابل مشاهده است که میزان استهلاک به میزان سرمایه انباشته شده، بستگی دارد.
در معادله زیر میتوان تاثیر سرمایهگذاری و استهلاک را نشان داد.
استهلاک — سرمایهگذاری = تغییرات در میزان سرمایهگذاری
△k=i−δk△k=i−δk
در معادله بالا، trianglektrianglek بیانگر میزان تغییرات در سرمایه انباشتهشده بین یکسال و سال آتی است. به علت برابری ii با sf(k)sf(k)، میتوان معادله بالا را به شکل زیر نوشت.
△k=sf(k)−δk△k=sf(k)−δk
در نمودار زیر میتوانید عوامل تشکیل دهنده این معادله (سرمایهگذاری و استهلاک) را به ازای مقادیر مختلف سرمایه انباشتهشده، مشاهده کنید. هرچه میزان سرمایه انباشتهشده بیشتر باشد، میزان استهلاک نیز بیشتر خواهد بود. همانطور که در نمودار زیر قابل بررسی است، در مقدار معینی از میزان سرمایه انباشتهشدهk∗k∗، میزان سرمایهگذاری برابر میزان استهلاک خواهد بود. اگر میزان سرمایه انباشتهشده اقتصاد در این نقطه قرار بگیرد، تغییر نخواهد کرد زیرا میزان سرمایهگذاری و استهلاک در تعادل قرار دارند.
یعنی در نقطه k∗k∗ مطابق محاسبات trianglektrianglek برابر صفر است. در نتیجه، میزان انباشت سرمایه و میزان تولید (k)f در طی زمان ثبات دارند و دچار افزایش یا کاهش نمیشوند. بنابراین، k∗k∗ «حالت پایدار ثابت » (Steady-state) سرمایه است. به ۲ علت، حالت پایدار ثابت، با اهمیت در نظر گرفته میشود.
همانطور که مشاهده شد، اقتصادی که در حالت پایدار ثابت باشد، در آن وضعیت باقی خواهد ماند. دلیل دوم اینکه، اقتصادی که در حالت پایدار ثابت قرار ندارد، در آن وضعیت قرار خواهد گرفت. یعنی فارغ از میزان سرمایه انباشتهشدهای که اقتصاد از اول داشته باشد، در نهایت در حالت پایدار ثابت، قرار میگیرد
به عبارتی، حالت پایدار ثابت، نشاندهنده تعادل بلندمدت در اقتصاد است. برای درک اینکه چگونه اقتصاد در نهایت در حالت پایدار ثابت قرار میگیرد، فرض کنید که اقتصاد میزان سرمایهای کمتر از سرمایه لازم برای حالت پایدار ثابت را داشته باشد. این سطح از سرمایه را با k1k1 نشان میدهیم. در اینصورت، میزان سرمایهگذاری بیشتر از میزان استهلاک است.
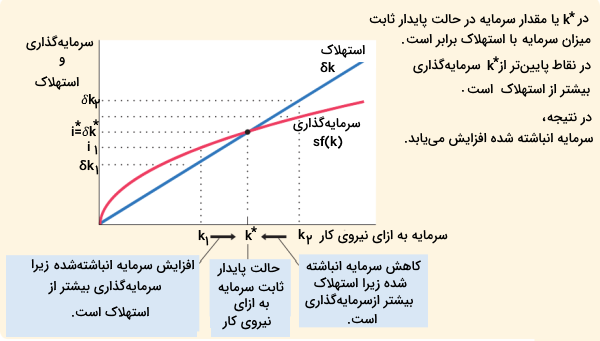
در طی زمان، میزان سرمایه افزایش پیدا میکند و این زیاد شدن به همراه تولید (f(k)f(k)) ادامهدار خواهد بود تا زمانی که به حالت پایدار ثابت (k∗k∗) برسد. از طرفی دیگر، فرض کنید که اقتصاد بیشتر از مقدار حالت پایدار ثابت سرمایه داشته باشد. برای مثال، اگر میزان سرمایه به اندازه k2k2 باشد. در اینصورت، میزان سرمایهگذاری کمتر از استهلاک خواهد بود. یعنی فرسوده شدن سرمایه در مقایسه با سرعت جایگزینی آن، کندتر صورت میگیرد. بنابراین، میزان سرمایه کاهش پیدا میکند و دوباره به حالت پایدار ثابت میرسد. زمانی که میزان سرمایه به حالت پایدار ثابت برسد، میزان سرمایهگذاری برابر میزان استهلاک خواهد بود و فشاری در جهت افزایش یا کاهش پیدا کردن بر میزان سرمایه وارد نمیشود.
مثال عددی از حالت پایدار ثابت در مدل سولو
در این قسمت با طرح یک مثال عددی با مدل سولو و چگونگی نزدیک شدن اقتصاد، به حالت پایدار ثابت آشنا میشویم. برای این مثال، تابع تولید را به شکل زیر فرض خواهیم کرد.
Y=K0.5×L0.5Y=K0.5×L0.5
تابع بکارگرفته شده از انواع تابعهای تولید کاب-داگلاس است. جهت بدست آوردن تابع تولید برحسب نیروی کار کافی است، هر دو سمت معادله را بر تعداد نیروی کار یا «LL» تقسیم کنیم. که در اینصورت، معادله، ساختاری به شکل زیر را به خود میگیرد.
YL=K0.5L0.5LYL=K0.5L0.5L
با اعمال تغییرات به معادله به شکل زیر دست پیدا میکنیم.
YL=(KL)0.5YL=(KL)0.5
همانطور که میدانیم، YL=yYL=y و KL=kKL=k بنابراین، میتوان معادله بالا را به شکل تبدیل کرد.
y=k0.5y=k0.5
که میتوان آنرا به صورت زیر هم نوشت.
y=√ky=k
این نوع از تابع تولید نشاندهنده این است که میزان تولید به ازای نیروی کار با ریشه دوم میزان سرمایه به ازای نیروی کار، برابری میکند. برای کامل کردن مثال، فرض کنید که ۳۰ درصد از میزان تولید ذخیره شود(s=o.3s=o.3) و اینکه ۱۰ درصد از سرمایه به صورت سالیانه (s=o.1s=o.1) مورد استهلاک قرار بگیرد و در ابتدای امر، در اقتصاد، میزان سرمایه به ازای نیروی کار، برابر ۴ ($s=o.1$s=o.1$) است.
با در نظر گرفتن این اعداد، میتوانیم بررسی کنیم که در گذر زمان در اقتصاد، چه اتفاقاتی رخ میدهد. در ابتدا، باید میزان تولید و تخصیص محصولات را در سال اول، با وجود ۴ واحد سرمایه به ازای نیروی کار، مورد توجه قرار دهیم. در ادامه، از گامهای زیر پیروی خواهیم کرد.
- مطابق تابع تولید، y=√ky=k، با ۴ واحد از سرمایه به ازای نیروی کار، به ۲ واحد تولید به ازای نیروی کار، دست پیدا میکنیم.
- ۳۰ درصد از میزان تولید، پسانداز و سرمایهگذاری میشود و ۷۰ درصد مورد مصرف قرار میگیرد. در نتیجه، i=0.6i=0.6 و c=1.4c=1.4 خواهند بود.
- از آنجاییکه، ۱۰ درصد از میزان سرمایه مستهلک میشود، δk=0.4δk=0.4 خواهد بود.
- با سرمایهگذاری ۰٫۶ و استهلاک ۰٫۴، میزان تغییرات در سرمایه برابر △k=0.2△k=0.2 خواهد بود.
بنابراین، اقتصاد در سال دوم فعالیت خود را با ۴٬۲ واحد سرمایه به ازای نیروی کار شروع میکند. میتوانیم این محاسبات را برای سال آتی نیز انجام دهیم. در جدول زیر میتوانید چگونگی پیشرفت اقتصاد را مشاهده کنید. هر سال، به علت بیشتر بودن سرمایهگذاری از استهلاک، سرمایه جدید اضافه شده و میزان تولید افزایش مییابد. در طی سالها، اقتصاد به حالت پایدار ثابت، با ۹ واحد از سرمایه به ازای نیروی کار میرسد. در این حالت پایدار ثابت، سرمایهگذاری ۰٫۹ دقیقاً میزان استهلاک ۰٫۹ را جبران میکند، بنابراین، میزان سرمایه و میزان تولید، دیگر رشدی را تجربه نخواهند کرد.
بررسی پیشرفت اقتصادی در یک جامعه، یکی از راههای پیدا کردن میزان سرمایه مورد نیاز حالت پایدار ثابت است اما روش دیگری نیز وجود دارد که با محاسبات کمتر نیز قابل انجام است. این معادله نشاندهنده چگونگی تغییرات kk در طی زمان است.
△k=sf(k)−δk△k=sf(k)−δk
از آنجاییکه، حالت پایدار ثابت، نشاندهنده مقداری از kk است که در آن، △k=0△k=0 است، میدانیم که:
0=sf(k∗)−δk∗0=sf(k∗)−δk∗
یا به صورت همسان، معادله به شکل زیر خواهد بود.
k∗f(k∗)=sδk∗f(k∗)=sδ
معادله بالا، فراهمکننده راهی برای یافتن میزان سرمایه به ازای نیروی کار در حالت پایدار ثابت (k^{*}) است. با جایگذاری عددها در تابع تولید معرفیشده در بالا، به تساوی زیر دست پیدا میکنیم.
k∗√k∗=0.30.1k∗k∗=0.30.1
هردو طرف معادله را به توان دو میرسانیم تا به معادله زیر دست پیدا کنیم.
k∗=9k∗=9
بنابراین، میزان سرمایه در حالت پایدار ثابت برابر ۹ واحد به ازای نیروی کار خواهد بود.
معجزه رشد اقتصادی ژاپن و آلمان
آلمان و ژاپن بیانکننده دو داستان موفقیت در رشد اقتصادی هستند. با اینکه این دو کشور هر دو جزو ابرقدرتهای اقتصادی به شمار میروند، در سال 1946 میلادی، اقتصاد هر دو این کشورها در وضعیت نامناسبی قرار داشت و جنگ جهانی دوم، اغلب سرمایههای این کشورها را نابود کرده بود. در سال ۱۹۴۶ میلادی، در هردوی کشورهای یادشده، میزان تولید به ازای هر فرد نصف میزان قبل از جنگ بود. اگرچه، در دهههای بعدی، این کشورها بیشترین رشدهای اقتصادی ثبتشده را تجربه کردند.
بین سالهای ۱۹۴۶ تا ۱۹۷۲ میلادی، در ژاپن، میزان رشد به ازای هر فرد برابر ۸٫۰ درصد در سال و ۶٫۵ درصد در سال در آلمان و در همین سالها، این مقدار برابر ۲٫۱ درصد در ایالات متحده آمریکا بود. در این دوره پس از جنگ، کشورهای اروپایی متعددی رشد اقتصادی قابل توجه را تجربه کردند. برای مثال، در دوره پس از جنگ، میزان محصول به ازای نیروی کار در فرانسه به صورت سالیانه ۴٫۶ درصد رشد و به صورت سالیانه در ایتالیا ۵٫۵ درصد رشد داشته است اما ژاپن و آلمان، کشورهایی بودند که از بیشترین صدمات در طی جنگ جهانی آسیب دیدند و پس از آن نیز، بیشترین رشد را داشتند.
بررسی رشد اقتصادی ژاپن و آلمان از دیدگاه مدل سولو
اقتصادی را در حالت پایدار ثابت، در نظر بگیرید. حال فرض کنید که در اثر جنگ، مقداری از سرمایههای آن تخریب شود. یعنی میزان سرمایه از k∗k∗ به k1k1 برسد. در این حالت، به صورت غیرمنتظرهای، میزان محصولات به سرعت کاهش پیدا میکند. در صورتی که نرخ پسانداز – کسر اختصاص یافته از میزان تولید به پسانداز و سرمایهگذاری – دستخوش تغییر نشود، اقتصاد، رشد بالایی را تجربه خواهد کرد.
میزان تولید و محصولات افزایش مییابد زیرا مطابق مدل سولو، در مقدار کمتر سرمایه، میزان سرمایه افزودهشده بیشتر از میزان سرمایه مستهلک شده است. این میزان رشد بالا افزایش پیدا میکند تا زمانیکه اقتصاد به حالت پایدار ثابت پیشین خود دست پیدا کند. در نتیجه، با اینکه از بین رفتن بخشی از سرمایه، به سرعت کاهش میزان تولید را در پی دارد، در ادامه، رشد اقتصادی بیشتر از میزان عادی، رخ خواهد داد.
معجزه رشد سریع در اقتصاد آلمان و ژاپن که اغلب مورد توجه رسانههای تجاری قرار میگیرد، مورد پیشبینیشده توسط مدل سولو برای کشورهایی است که در اثر جنگ، در آنها، سرمایه به میزان بسیاری کاهش پیدا کرده است. پس از تجربه میزان رشد بالا در دوران پس از جنگ، ژاپن و آلمان هردو رشدهای تعدیلشدهتری را تجربه کردند که شباهت بیشتری به میزان رشد ایالات متحده داشت.
از سال ۱۹۷۲ تا سال ۲۰۰۰ میلادی، ژاپن میزان تولید سرانه با نرخ ۲٫۴ درصد سالیانه و آلمان میزان تولید سرانه ۱٫۸ درصدی را در مقایسه با رشد ۲٫۱ درصدی در ایالات متحده آمریکا، تجربه کردهاند. این پدیده، نیز توسط مدل سولو پیشبینی شده است. با نزدیکتر شدن اقتصاد به حالت پایدار ثابت خود، این اقتصاد دیگر تجربهکننده رشدهای بیش از حد معمول که در نتیجه بازگشت به حالت پایدار ثابت بوجود میآیند، نخواهد بود. البته این موارد نباید موجب شود که فردی آسیبها و تخریبها بوجود آمده از جنگ را مطلوب در نظر بگیرد.
رشد اقتصادی سریع در ژاپن و ایالات متحده آمریکا در دوران پس از جنگ، موجب شد این کشورها در وضعیتی قرار بگیرند که بدون وقوع جنگ نیز، در آن وضعیت قرار میگرفتند. بهعلاوه، برخلاف ژاپن و آلمان، بسیاری از کشورهای آسیبدیده از جنگ جهانی، به جنگ داخلی و بیثباتی سیاسی دچار شدند که از وقوع رشدهای اقتصادی آتی نیز جلوگیری میکرد.
تاثیر پسانداز بر رشد اقتصادی چگونه است؟
تشریح دلایل رشد اقتصادی ژاپن و آلمانی به سادگی موارد عنوانشده در بالا نیست. مورد دیگری که باید به آن توجه شود، این است که هم آلمان و هم ژاپن در مقایسه با ایالات متحده آمریکا، درصد بیشتری از میزان تولیدات خود را سرمایهگذاری و پسانداز میکنند. برای درک بهتر تفاوتهای بینالمللی در عملکردهای اقتصادی، باید تفاوتهای نرخهای مختلف پسانداز را مورد توجه قرار دهیم
باید در نظر بگیرید که با افزایش نرخ پسانداز در یک اقتصاد، چه اتفاقی رخ میدهد. در نمودار زیر میتوانید نمونهای از این تغییر را مشاهده کنید. فرض میکنیم که اقتصاد در حالت پایدار ثابت با نرخ پسانداز s1s1 و سرمایه k∗1k1∗ قرار داشته باشد. با رسیدن نرخ پسانداز از s1s1 به s2s2، منحنی sf(k)sf(k) به سمت بالا انتقال پیدا میکند.
در نرخ پسانداز ابتدایی s1s1 و میزان سرمایه ابتدایی k∗1k1∗ میزان سرمایهگذاری، میزان استهلاک را پوشش خواهد داد. به سرعت پس از افزایش پیدا کردن نرخ پسانداز، سرمایهگذاری بیشتر میشود اما میزان سرمایه و میزان استهلاک بدون تغییر باقی میمانند. بنابراین، سرمایهگذاری بیشتر از استهلاک خواهد بود. میزان سرمایه به تدریج افزایش پیدا میکند تا جایی که اقتصاد به حالت پایدار ثابت جدید k∗2k2∗ میرسد که در مقایسه با حالت پایدار ثابت پیشین، میزان سرمایه و میزان تولید بیشتری دارد.
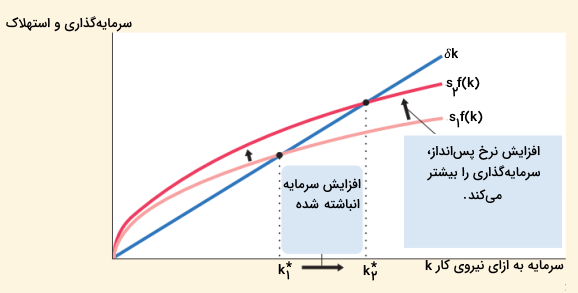
از مدل سولو در مییابیم که نرخ پسانداز عاملی تعیینکننده در میزان سرمایه حالت پایدار ثابت به شمار میرود. در صورت بالاتر بودن نرخ پسانداز، اقتصاد میزان سرمایه و سطحی بالا از تولید را در حالت پایدار ثابت خواهد داشت و برعکس. این مورد بیانگر بسیاری از مباحثات پیرامون سیاستهای مالی است. همانطور که میدانید، کسری بودجه دولت میتواند مقدار پسانداز ملی را کاهش دهد و افزایش مخارج بخش دولتی، کاهش پیدا کردن مخارج و سرمایهگذاریهای بخش خصوصی را به همراه داشته باشد. حال، به خوبی قابل مشاهده است که پیامدهای بلندمدت نرخ پسانداز کاهشیافته، کاهش سرمایه و کاهش درآمد ملی هستند.
به همین دلیل، بسیاری از اقتصاددانان به کسری بودجههای مداوم، نقد وارد میکنند. سیاستگذاریهای تغییردهنده نرخ رشد درآمد سرانه حالت پایدار ثابت، «اثر رشد» (Growth Effect) خواهد داشت، از طرفی دیگر، نرخ پسانداز بالاتر، «اثر سطحی» (Level Effect) دارد زیرا تنها سطح درآمد سرانه و نه نرخ رشد آن، تحت تاثیر نرخ پسانداز در حالت پایدار ثابت قرار میگیرد.
حال که به رابطه تعاملی میان پسانداز و رشد پی بردیم، بهتر میتوانیم عملکرد اقتصادی آلمان و ژاپن را بعد از جنگ جهانی دوم تشریح کنیم. در این کشورها، نه تنها میزان سرمایه ابتدایی اندک بود بلکه به علت جنگ، مقدار سرمایه حالت پایدار ثابت به علت پس انداز بالا، قابل توجه به شمار میرفت. هر دوی این موارد موجب میشدند که این ۲ کشور در دهههای ۱۹۵۰ و ۱۹۶۰ میلادی، رشد چشمگیری را تجربه کنند.
قانون طلایی سطح سرمایه
تا اینجا، از مدل سولو برای بررسی چگونگی تعیینشدن میزان سرمایه و درآمد حالت پایدار ثابت توسط نرخ پسانداز و سرمایهگذاری استفاده کردهایم. این تحلیل ممکن است باعث شود که شما فکر کنید که پس انداز بالا، همیشه موردی مثبت است زیرا درآمد بیشتری را به همراه دارد. در همین حال، فرض کنید که کشوری نرخ پسانداز ۱۰۰ درصدی داشته باشد. یعنی بیشترین سرمایه و بالاترین درآمد ممکن، کسب شود. اگر تمام درآمد، پسانداز شود و هیچ بخشی از آن مصرف نشود، چه فایدهای خواهد داشت؟ در این بخش، از مدل سولو برای یافتن میزان بهینه سرمایه انباشتهشده از دیدگاه رفاه اقتصادی استفاده میشود
مقایسه حالتهای پایدار ثابت
برای سادهبودن تحلیل، فرض کنید که سیاستگذار بتواند نرخ پس انداز را در هر سطحی قرار دهد. با تعیین نرخ پسانداز، سیاستگذار موفق به تعیین حالت پایدار ثابت میشود. سیاستگذار باید کدام حالت پایدار ثابت را انتخاب کند؟
هدف سیاستگذار، رفاه حداکثری شهروندان تشکیلدهنده جامعه است. شهروندان به تنهایی، اهمیتی برای میزان سرمایه در اقتصاد یا میزان تولید، قائل نمیشوند. آنها تنها به مقدار کالاها و خدماتی که توانایی مصرفشان را دارند، توجه میکنند. بنابراین، سیاستگذار باید حالت پایدار ثابتی با بیشترین میزان مصرف را انتخاب کند. میزان kk حداکثرکننده مصرف قانون طلایی سرمایه نامیده میشود و آنرا به صورت k∗gkg∗ نشان میدهنده که در آن «gg» مخفف «GoldGold» است.
چگونه تعیین کنیم که اقتصادی در حالت قانون طلایی قرار دارد یا خیر؟
برای تعیین این مورد، باید ابتدا، میزان مصرف به ازای نیروی کار را در حالت پایدار ثابت، تعیین کنیم. سپس، میتوانیم تشخیص دهیم که کدام حالت پایدار ثابت بیشترین میزان مصرف را به همراه خواهد داشت. برای یافتن میزان مصرف به ازای نیروی کار حالت پایدار ثابت، به حساب درآمد ملی رجوع میکنیم.
y=c+iy=c+i
و ساختار آنرا به شکل زیر تغییر میدهیم.
c=y−ic=y−i
مصرف را معادل میزان تولیدی که از آن سرمایه گذاری کسر شده است، در نظر میگیریم. از آنجاییکه هدف دستیابی به مقدار مصرف حالت پایدار ثابت است، در معادله بالا، میزان تولید و سرمایهگذاری حالت پایدار ثابت را جایگزین میکنیم. میزان تولید به ازای نیروی کارِ حالت پایدار ثابت برابر f(k∗)f(k∗) است که در آن k∗k∗ همان میزان سرمایه به ازای نیروی کار حالت پایدار ثابت به شمار میرود. همچنین، به علت تغییرناپذیری میزان سرمایه در حالت پایدار ثابت، سرمایهگذاری برابر میزان استهلاک δk∗δk∗ خواهد بود. با جایگزین کردن f(k∗)f(k∗) به جای yy و δk∗δk∗ به جای ii، میتوان مصرف به ازای نیروی کار حالت پایدار ثابت را به شکل زیر نوشت.
c∗=f(k∗)−δk∗c∗=f(k∗)−δk∗
مطابق معادله بالا، مصرف حالت پایدار ثابت، میزان تولیدات حالت پایدار ثابت باقیمانده، بعد از پرداخت استهلاک حالت پایدار ثابت است. این معادله نشان میدهد که افزایش میزان سرمایه حالت پایدار ثابت، ۲ اثر متضاد بر مصرف حالت پایدار ثابت دارد. از طرفی، سرمایه بیشتر به معنی تولید بیشتر خواهد بود. از طرفی دیگر، سرمایه بیشتر به این معنی است که باید از میزان تولیدات بیشتری برای جایگزینی سرمایه فرسوده شده استفاده کرد.
در نمودار زیر میتوانید میزان تولید حالت پایدار ثابت و میزان استهلاک حالت پایدار ثابت را به عنوان تابعی از میزان سرمایه حالت پایدار ثابت مشاهده کنید. میزان مصرف حالت پایدار ثابت نشاندهنده فاصله میان میزان تولید و استهلاک است. مطابق این نمودار، تنها یک سطح از میزان سرمایه وجود دارد – سطح سرمایه قانون طلایی یا k∗gkg∗ – که حداکثرکننده میزان مصرف است.
با مقایسه حالتهای پایدار ثابت، باید بخاطر داشته باشیم که سطح بالاتر سرمایه هم مقدار تولید و هم میزان استهلاک را تحت تاثیر قرار خواهد داد. اگر مقدار سرمایه پایینتر از سطح قانون طلایی باشد، افزایش میزان سرمایه، تولید را بیشتر از استهلاک افزایش میدهد. بنابراین، مصرف هم زیادتر میشود.
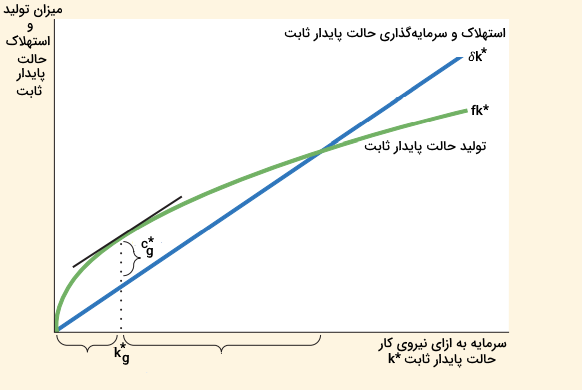
در این نمونه، تابع تولید در مقایسه با خط δk∗δk∗ شیب بیشتری دارد، بنابراین فاصله میان این دو منحنی – که معادل مصرف است – با افزایش k∗k∗ بیشتر میشود. از طرفی دیگر، اگر میزان سرمایه بالاتر از سطح قانون طلایی باشد، افزایش سرمایه، مصرف را کاهش خواهد داد، زیرا افزایش تولید کمتر از افزایش بوجود آمده میزان استهلاک است. در این حالت، تابع تولید کمشیبتر از خط δk∗δk∗ است، بنابراین فاصله میان این منحنیها، با افزایش k∗k∗ کاهش پیدا میکند.
در میزان سرمایه سطح قانون طلایی، تابع تولید و خط δk∗δk∗ شیب یکسانی دارند و مقدار مصرف نیز بیشینه است. حال میتوانیم شرطی را استخراج کنیم که نشاندهنده مقدار سرمایه در شرایط برقراری قانون طلایی باشد. شیب تابع تولید همان «تولید نهایی سرمایه» (MPK) است. شیب خط δk∗δk∗ برابر δδ است. شیب این خط و شیب تابع تولید در k∗gkg∗ با یکدیگر برابر خواهند بود. بنابراین، قاعده طلایی توسط معادله زیر تعریف میشود.
MPK=δMPK=δ
زمانی که سرمایه به اندازه سرمایه مورد نیاز برای قانون طلایی باشد، تولید نهایی سرمایه برابر نرخ استهلاک خواهد بود. برای درک این مسئله از بعدی دیگر، فرض کنید که میزان سرمایه در اقتصاد برابر سرمایه در حالت پایدار ثابت k∗k∗ باشد و سیاستگذار قصد داشته باشد که آنرا به k∗+1k∗+1 برساند.
میزان تولید افزودهشده ناشی از این افزایش سرمایه برابر f(k∗+1)−f(k∗)f(k∗+1)−f(k∗) یا همان تولید نهایی سرمایه است. اضافه استهلاک بوجود آمده ناشی از داشتن یک واحد سرمایه همان میزان استهلاک است. بنابراین، تاثیر این واحد اضافه سرمایه بر مصرف برابر MPK−δMPK−δ است. اگر این مقدار مثبت باشد، افزایش سرمایه، افزایش مصرف را به همراه خواهد داشت. در نتیجه، k∗k∗ باید پایینتر از سطح قاعده طلایی باشد.
نظر مدل سولو درباره رابطه میان پسانداز و رشد اقتصادی
در مدل سولو، پسانداز بیشتر، رشد سریعتری را به همراه خواهد داشت اما به صورت موقتی. افزایش نرخ پسانداز تنها تا زمان رسیدن اقتصاد به حالت پایدار ثابت جدید، رشد اقتصادی را افزایش میدهد. اگر اقتصاد، نرخ پسانداز بالا را حفظ کند، میزان قابلتوجهی سرمایه و تولید خواهد داشت اما نرخ رشد همیشه بالا نخواهد ماند./ فرادرس


